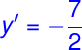Category: Integral Calculus
"Published in Newark, California, USA"
Evaluate
Solution:
Consider the given equation above
Convert each term into their equivalent exponential power, we have
All terms can be integrated by integration of powers
Substitute the value of limits and therefore, the answer is

This website will show the principles of solving Math problems in Arithmetic, Algebra, Plane Geometry, Solid Geometry, Analytic Geometry, Trigonometry, Differential Calculus, Integral Calculus, Statistics, Differential Equations, Physics, Mechanics, Strength of Materials, and Chemical Engineering Math that we are using anywhere in everyday life. This website is also about the derivation of common formulas and equations. (Founded on September 28, 2012 in Newark, California, USA)
Tuesday, 28 May 2013
Monday, 27 May 2013
Partial Differentiation
Category: Differential Calculus, Algebra
"Published in Newark, California, USA"
If
show that
Solution:
Consider the given equation above
Take the partial derivative with respect to x, consider y as a constant, we have
Consider the given equation above again
Take the partial derivative with respect to y, consider x as a constant, we have
If
then
Therefore,
"Published in Newark, California, USA"
If
show that
Solution:
Consider the given equation above
Take the partial derivative with respect to x, consider y as a constant, we have
Consider the given equation above again
Take the partial derivative with respect to y, consider x as a constant, we have
If
then
Therefore,
Sunday, 26 May 2013
Differentiation - First Derivative
Category: Differential Calculus, Algebra
"Published in Newark, California, USA"
Find y' for the given value of x for
Solution:
Consider the given equation above
Simplify the numerator in order to avoid the confusion later for differentiation, we have
Take the derivative of the above equation with respect to x
If x = 1, then the value of y' is equal to
"Published in Newark, California, USA"
Find y' for the given value of x for
Solution:
Consider the given equation above
Simplify the numerator in order to avoid the confusion later for differentiation, we have
Take the derivative of the above equation with respect to x
If x = 1, then the value of y' is equal to
Subscribe to:
Comments (Atom)