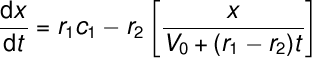"Published in Newark, California, USA"
A tank contains 80 gals. of pure water. A brine solution with 2 lbs/gal of salt enters at 2 gals/min, and the well-stirred mixture leaves at the same rate. Find (a) the amount of salt in the tank at any time, and (b) the time at which the brine leaving will contain 1 lb/gal of salt.
Solution:
The first thing that we have to do is to analyze and illustrate the given word problem as follows
 |
| Photo by Math Principles in Everyday Life |
Since the given word problem involves the mixture of non-reactive fluids, the working equation will be as follows
where
r1 = volumetric flow rate at the entrance
c1 = concentration of substance at the entrance
r2 = volumetric flow rate at the exit
c2 = concentration of substance at the exit
Since c2 is usually not given in the problem, we can rewrite the above equation as follows
where
x = the amount of salt at time t
V = final volume of a solution at time t
but
where
V0 is the initial volume of solution at t = 0
Therefore, the final working equation will be
In the given word problem, we know that
r1 = 2 gals/min
c1 = 2 lbs/gal
r2 = 2 gals/min
V0 = 80 gals
x0 = 0 lbs of salt (pure water)
then the above equation becomes
Since the above equation is a first order, first degree linear equation, then the integrating factor will be equal to
The general solution of the above equation is
(a) If x = 0 lbs of salt (pure water) at t = 0, then the value of C is
Therefore, the particular solution of the above equation or the amount of salt in the tank at time t is
(b) If c2 = 1 lb/gal, then t will be equal to
Since x is not given, then we can get the value of x using the final concentration of the brine and the volume of a tank as follows
Substitute the value of x to the above equation, we have
Take natural logarithm on both sides of the equation
which is equal to