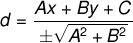"Published in Newark, California, USA"
Find the equation of a circle whose center on the line y = x, tangent to y = 5, and its radius is 2.
Solution:
To illustrate the problem, it is better to draw the figure as follows
 |
| Photo by Math Principles in Everyday Life |
In this problem, the center of a circle is unknown and we need to solve it. Since the radius of a circle is given, then we can solve for the coordinates of the center by using the perpendicular distance of a point to the line formula as follows
Substitute the coefficients of the equation of a line that is tangent to a circle, we have
If we choose a negative sign for the radical, then the above equation becomes
Substitute the values of the coordinates of the center of a circle to the above equation, we have
Since the center of a circle is located along the line y = x, then it follows that h = k = 3.
Therefore, the equation of a circle is
If we choose a positive sign for the radical, then the above equation becomes
Since the center of a circle is located along the line y = x, then it follows that h = k = 7.
Therefore, the equation of a circle is