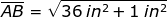"Published in Newark, California, USA"
A right prism of altitude 7 in. and square base 6 in. on an edge is cut by a plane forming section ABCD as shown. (a) Find the length of the diagonal AC. (b) Find angle ABC. (c) Find the area of section ABCD. (d) Find the angle which the plane of the section ABCD makes with the plane of the base.
 |
| Photo by Math Principles in Everyday Life |
Solution:
To understand more the problem, it is better to label further the figure as follows
 |
| Photo by Math Principles in Everyday Life |
From point A, draw four line segments which are perpendicular to the lateral edges of a prism so that plane AEFG is parallel to the base of a prism.
(a) The length of AC which is the diagonal of a plane section is
(b) By Pythagorean Theorem, the length of AB is
By Pythagorean Theorem, the length of BC is
Therefore, by Cosine Law, ∠ABC is
or
(c) Since plane ABCD is a parallelogram as you can see from the figure, therefore, the area of plane ABCD is
(d) The angle which the plane of the section ABCD makes with the plane of the base is
or