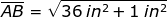"Published in Vacaville, California, USA"
In the figure is shown a block of wood in the form of a right prism whose bases are right triangles. A cylindrical auger hole of diameter 2 in. is bored through the block. If the elements of the cylindrical hole are perpendicular to face ABEF and if the lateral surface of the cylindrical hole is tangent to face ABCD, find the volume removed.
 |
| Photo by Math Principles in Everyday Life |
Solution:
Did you notice that the altitude or length of a right triangular prism is not given in the problem? Well, that's fine because we don't need it in the problem. If the word problem says "If the elements of the cylindrical hole are perpendicular to face ABEF and if the lateral surface of the cylindrical hole is tangent to face ABCD,..", then the side view of the section will be like this
 |
| Photo by Math Principles in Everyday Life |
The darker section is a truncated right circular cylinder because the two bases are not equal and their altitudes or elements are not equal. We have to get the average of their altitudes first before we can solve for the volume of a cylinder. By similar triangles, the other altitude of a cylinder is
Therefore, the amount of a cylindrical auger hole removed from a prism which is the volume of a truncated right circular cylinder is