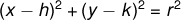Finding Equation - Circle, 4

Category: Analytic Geometry, Plane Geometry

"Published in Newark, California, USA"

Find the equation of a circle that is tangent to the line 4x - 3y + 10 = 0 and its center at (5, 5).

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The radius of a circle can be solved by using the perpendicular distance of a point to the line formula as follows

where A, B, and C are the coefficients of the equation of a given line. Hence, the above equation becomes
 

 

   
Since the coefficient of 10 is positive, then it follows that the sign of a radical is negative. Take the opposite sign of 10.
 

 

 

Substitute the values of x and y from the coordinates of a center of a circle, we have

 

 

 

   
The radius of a circle is always a positive value. We need to take the absolute value for that one. Hence, r = 3.
 
Therefore, the equation of a circle is
 

 

 

 

Finding Equation - Circle, 3

Category: Analytic Geometry, Plane Geometry

"Published in Newark, California, USA"

Find the equation of a circle having as diameter the line segment from (-1, 1) to (3, 4).

Solution: 

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The first thing that we need to do is to get the center of a circle by using the midpoint formula of the two points as follows

Hence, the center of a circle is C (1, 5/2).

Next, get the radius of a circle by using the distance formula of two points as follows 

Therefore, the equation of a circle is

 

Finding Equation - Circle, 2

Category: Analytic Geometry, Plane Geometry

"Published in Vacaville, California, USA"

Find the equation of a circle if the endpoints of a diameter are A (-1, 3) and B (7, -5).

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The first thing that we need to do is to get the center of a circle by using the midpoint formula of the two points as follows

 

 

 

 

 

 

Hence, the center of a circle is C (3, -1).

Next, get the radius of a circle by using the distance formula of two points as follows
 

 

 

 

 

   
Therefore, the equation of a circle is
 

 

 

 

Finding Equation - Circle

Category: Analytic Geometry, Plane Geometry, Algebra

"Published in Newark, California, USA"

Find the equation of a circle that is tangent to both axes, center in second quadrant and radius is 2.

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

When you say tangent, it is perpendicular. In this case the radius of a circle is perpendicular to x-axis and y-axis. If a circle is located at the second quadrant, the center is C (-2, 2). Therefore, the equation of a circle is