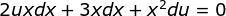"Published in Vacaville, California, USA"
Find the particular solution for
in which y = 3 when x = 1.
Solution:
Consider the given equation above
Did you notice that the given equation cannot be solved by separation of variables? The algebraic functions are the combination of x and y in the group and there's no way that we can separate x and y.
This type of differential equation is a homogeneous function. Let's consider this procedure in solving the given equation as follows
Let
so that
Substitute the values of y and dy to the given equation, we have
The resulting equation can now be separated by separation of variables as follows
Integrate on both sides of the equation, we have
Take the inverse natural logarithm on both sides of the equation, we have
But
Hence, the above equation becomes
Substitute the value of x and y in order to get the value of C as follows
Therefore, the particular solution is
There's another way in getting the particular solution of the given equation above as follows
Integrate both sides of the equation, we have
Substitute the value of x and y in order to get the value of C as follows
Therefore, the particular solution is
