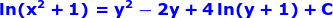Approximation - Error Problem

Category: Differential Calculus, Solid Geometry

"Published in Newark, California, USA"

The altitude of a certain right circular cone is the same as the radius of the base, and is measured as 5 inches with a possible error of 0.02 inch. Find approximately the percentage error in the calculated value of the volume.

Solution:

From the description of a problem, it is an approximation and error problem because it involves the difference of the dimensions of a right circular cone as well  as the difference of the volume. 
 

Photo by Math Principles in Everyday Life

 
The volume of a right circular cone is calculated as

but r = h

Take the differentials on both sides, we have

The original volume of the right circular cone is calculated as

Therefore, the percent of error is calculated as

% Error = (± 0.012)(100) = 1.2%

Maximum Minimum Problem

Category: Differential Calculus

"Published in Newark, California, USA"

A farmer estimates that if he digs his potatoes now, he will have 120 bushels, which he can sell at $1.75 per bushel. If he expects his crop to increase 8 bushels per week, but the price to drop 5 cents per bushel per week, in how many weeks should he sell to realize the maximum amount for his crop?

Solution:  

Let x be the number of bushels of potatoes per week

Let y be the price change of potatoes per bushels per week

Let t be the time/period of harvesting potatoes in weeks

Let C be the total cost of the potatoes

By analyzing the problem above, initially, there are 120 bushels of potatoes that the farmer can sell at $1.75 per bushel.

Total Cost of Potatoes = (Total Number of Potatoes in bushels)(Total Price of Potatoes per bushel)

                    C (initial) = (120)($1.75)

At the next statement, his crop will increase 8 bushels per week. The total number of potatoes in bushels can be written as

      Total Number of Potatoes = 120 + xt

and there will be a change of price of potatoes per bushels per week. The total price of potatoes per bushel can be written as

    Total Price of Potatoes per bushel = $1.75 + yt

Therefore, we can now write the working equation of Total Cost of Potatoes as follows:

Next we have to take the derivative of the above equation with respect to t, we have

You notice that we use the derivative of the product of two functions. Next, set dC/dt = 0 because we want to maximize the total cost of potatoes. 

   
Therefore, he should sell his potatoes in 10 weeks.

Graphical Sketch - Circle

Category: Analytic Geometry, Plane Geometry

"Published in Newark, California, USA"

Given the equation of a circle:

Find its center and radius. Sketch the graph.

Solution:

From the given equation,

This equation represents a circle because the coefficients of x² and y² are the same and no xy term in the general equation of a conic section. Circle is also a type of conic section. Our goal right now is to find its center and radius. Since x² and y² have their coefficients, we have to divide both sides of the equation by 4 in order to eliminate their coefficients, we have

Group the above equation according to their variables and transpose the coefficient to the right side of the equation,

Next, let's do the completing the square for x² and y²,

The above equation can be written as

In order to get the center and radius of a circle, the equation must be simplified into standard form. The above equation is now in standard form.

To get the center of a circle,

                    x - 1 = 0                  y + 2 = 0          

                         x = 1                        y = -2

Therefore, C(1, -2)

The radius of a circle is 3.

We can now sketch the graph using the above results.

Photo by Math Principles in Everyday Life

Temperature Conversion Equation

Category: Algebra, Chemical Engineering Math

"Published in Newark, California, USA"

The students are performing their experiment in Physics Lab to observe and record the temperature of freezing water and boiling water with the use of ºC thermometer and ºF thermometer.  At their first experiment, the two thermometers are dipped together in a beaker filled with water. If a beaker is placed inside the freezer, the water is starting to freeze at 0 ºC and 32 ºF. At their second experiment, the two thermometers are dipped together in another beaker filled with water. If a beaker is placed at the top of the heating plate, the water is starting to boil at 100 ºC and 212 ºF. From the temperature readings of two thermometers, how do you convert the temperature reading from ºC to ºF and vice versa? At what temperature is the ºC and ºF readings will be equal?

Solution:

The first thing that you have to do is to draw the two thermometers with the observed temperature readings for the freezing point and boiling point of water.

Photo by Math Principles in Everyday Life

Next, we have to assign the unknown readings at the middle of the two thermometers. From the given figure, the problem type is likely the ratio and proportion. Further label the figure, we have,

Photo by Math Principles in Everyday Life

Using the ratio and proportion,

or we can rewrite the above equation as

If ^oF = ^oC,

                                        ^oF = - 40

Variable Separation

Category: Differential Equations, Integral Calculus

"Published in Newark, California, USA"

Find the general solution for the equation:

Solution:

If you examine the above equation, it is a differential equation because it contains the differentials like dx and dy. Our goal is to eliminate the differentials by integration but before that, let's examine the above equation. We have to do first the grouping at the right side of the equation and then factor all the terms if there are any common factors. The above equation can be written as

You noticed that we are applying the principles of factoring for the above equation. You must know the principles of Algebra, Trigonometry, and Calculus very well in solving Differential Equations. Next, we want to eliminate y at the left side of the equation and also we want to eliminate x at the right side of the equation. If you will divide both sides of the equation by (y + 1)(x² +1), then the above equation becomes

Now, looking at the right side of the equation, the exponential degree at the numerator is greater than at the denominator. We have to do the division first as follows
                                         

The above equation can be written as

Next, integrate on both sides of the equation

Multiply both sides by 2 to eliminate the fraction, we have

A constant (C) multiply by any number is still a constant.

Note: In some cases, C can be written as ln C after the integration. It's up to you. The natural logarithm of any constant is still a constant. 

Deriving Half Angle Formula

Category: Trigonometry

"Published in Newark, California, USA"

Last October 24, 2012, we did the derivation of Double Angle Formula. Right now, we will derive the formulas for Half Angle Formula from the formulas of Double Angle Formula. 

Let's consider this one,

but 
 

 

 
then the above equation becomes
 

 

 

If A = 2θ, then θ = ½ A

Take the square root on both sides of the equation,

Again, let's consider this one,

but

then the above equation becomes
 

 

 

 

If A = 2θ, then θ = ½ A

Take the square root on both sides of the equation,

How about for Tangent function? Well, let's derive for Tangent function. We know that

You can consider the above formula for Tangent function but there's a rule in Mathematics that the denominator must be free from radicals. Let's rationalize the denominator as follows: