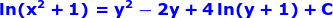Variable Separation

Category: Differential Equations, Integral Calculus

"Published in Newark, California, USA"

Find the general solution for the equation:

Solution:

If you examine the above equation, it is a differential equation because it contains the differentials like dx and dy. Our goal is to eliminate the differentials by integration but before that, let's examine the above equation. We have to do first the grouping at the right side of the equation and then factor all the terms if there are any common factors. The above equation can be written as

You noticed that we are applying the principles of factoring for the above equation. You must know the principles of Algebra, Trigonometry, and Calculus very well in solving Differential Equations. Next, we want to eliminate y at the left side of the equation and also we want to eliminate x at the right side of the equation. If you will divide both sides of the equation by (y + 1)(x² +1), then the above equation becomes

Now, looking at the right side of the equation, the exponential degree at the numerator is greater than at the denominator. We have to do the division first as follows
                                         

The above equation can be written as

Next, integrate on both sides of the equation

Multiply both sides by 2 to eliminate the fraction, we have

A constant (C) multiply by any number is still a constant.

Note: In some cases, C can be written as ln C after the integration. It's up to you. The natural logarithm of any constant is still a constant. 

Deriving Half Angle Formula

Category: Trigonometry

"Published in Newark, California, USA"

Last October 24, 2012, we did the derivation of Double Angle Formula. Right now, we will derive the formulas for Half Angle Formula from the formulas of Double Angle Formula. 

Let's consider this one,

but 
 

 

 
then the above equation becomes
 

 

 

If A = 2θ, then θ = ½ A

Take the square root on both sides of the equation,

Again, let's consider this one,

but

then the above equation becomes
 

 

 

 

If A = 2θ, then θ = ½ A

Take the square root on both sides of the equation,

How about for Tangent function? Well, let's derive for Tangent function. We know that

You can consider the above formula for Tangent function but there's a rule in Mathematics that the denominator must be free from radicals. Let's rationalize the denominator as follows:

Proving Basic Trigonometric Identity

Category: Trigonometry, Plane Geometry

"Published in Newark, California, USA"

Prove that:

    
Solution:
 
Let's consider the right triangle
 

Photo by Math Principles in Everyday life

 

We know that 

and 

From Pythagorean Theorem,

divide both sides of the equation by c², we have

                                 or

Therefore,