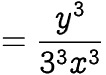Evaluating Inverse Trigonometric Functions

Category: Trigonometry

"Published in Newark, California, USA"

Evaluate, using principal values for the inverse functions involved

Solution:

The given equation above involves with inverse trigonometric functions. Each inverse trigonometric functions represents an angle. We can get the value of the above equation without using a calculator as follows

Let 

Express the above trigonometric function in a right triangle

Photo by Math Principles in Everyday Life

From the figure above, we can find the other trigonometric functions as follows

Let 

Express the above trigonometric function in a right triangle

Picture by Math Principles in Everyday Life

From the figure above, we can find the other trigonometric functions as follows

Now, consider the given equation

Rewrite the above equation as follows

Finally, substitute the value of each trigonometric functions to the above equation as follows

Algebraic Operations - Exponential Fractions

Category: Algebra

"Published in Newark, California, USA"

Perform the indicated operations and simplify:

Solution:

Consider the above equation

Since the terms in the numerator and denominator are monomial and have the same term which are 3, x, and y, then we can apply the laws of exponents as follows

Indeterminate Form - Zero Times Infinity

Category: Differential Calculus, Trigonometry

"Published in Newark, California, USA"

Evaluate the limit for

Solution:

Consider the given equation

Substitute the value of x to the above equation, we have

Since the answer is ∞∙0 which is also another type of Indeterminate Form, it is not accepted in Mathematics as a final answer. We know that any number multiply by zero is always equal to zero but there's an exception, which is infinity. Therefore, we cannot say that infinity times zero is zero. In this type of Indeterminate Form, you cannot use the L'Hopital's Rule because the L'Hopital's Rule is applicable for the Indeterminate Forms like 0/0 and ∞/∞. In this case, let's rewrite the given equation as follows

Substitute the value of x to the above equation, we have

Since the Indeterminate Form at this time is ∞/∞, then we can apply the L'Hopital's Rule to the above equation as follows

Since the trigonometric functions at the above equation are all cancelled and the constant is left, then we cannot substitute the value of x. Therefore,