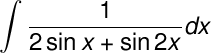Binomial Theorem

Category: Algebra, Arithmetic

"Published in Newark, California, USA"

Evaluate 

without using a calculator.

Solution:

Consider the given number

Rewrite and expand the given number as follows

It is better to convert the decimal number into its equivalent fraction for the given number 

Next, use the Binomial Theorem to expand the given number as follows

Get the Least Common Denominator (LCD) for all the fractions and simplify as follows

Convert the fraction into its equivalent decimal number as follows

Therefore,

Check:

If you will use a scientific calculator,

which is almost the same as the final answer.

More Integration Procedures, 6

Category: Integral Calculus, Trigonometry

"Published in Suisun City, California, USA"

Evaluate

Solution:

Consider the given above equation

Convert the double angle function into a single angle function as follows

Since the denominator contains trigonometric functions, then we have to use the Miscellaneous Substitution method. On December 17, 2012, we discussed and derived the equations for Miscellaneous Substitution as follows

Let 

Substitute the above values to the given equation above, we have

but

Therefore,

Maximum Minimum Problem, 4

Category: Differential Calculus, Plane Geometry

"Published in Suisun City, California, USA"

Find the area of the largest rectangle that can be inscribed in a right triangle with legs of lengths 3 cm and 4 cm if two sides of the rectangle lie along the legs as shown in the figure.

Photo by Math Principles in Everyday Life

Solution:

Consider the given figure above and label further as follows

Photo by Math Principles in Everyday Life

                               Area of Rectangle = Length x Width

Next, we need to use similar triangles in order to solve for the value of y as follows

Substitute the value of y to the above equation, we have

Take the derivative on both sides of the equation with respect to x, we have

Set dA/dx = 0 because we want to get the maximum area of the rectangle inscribed in a right triangle as follows

Consider

Substitute the value of x to the above equation, we have

Therefore, the area of the largest rectangle is