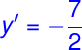Category: Differential Calculus, Algebra
"Published in Newark, California, USA"
If
show that
Solution:
Consider the given equation above
Take the partial derivative with respect to x, consider y as a constant, we have
Consider the given equation above again
Take the partial derivative with respect to y, consider x as a constant, we have
If
then
Therefore,

This website will show the principles of solving Math problems in Arithmetic, Algebra, Plane Geometry, Solid Geometry, Analytic Geometry, Trigonometry, Differential Calculus, Integral Calculus, Statistics, Differential Equations, Physics, Mechanics, Strength of Materials, and Chemical Engineering Math that we are using anywhere in everyday life. This website is also about the derivation of common formulas and equations. (Founded on September 28, 2012 in Newark, California, USA)
Monday, May 27, 2013
Sunday, May 26, 2013
Differentiation - First Derivative
Category: Differential Calculus, Algebra
"Published in Newark, California, USA"
Find y' for the given value of x for
Solution:
Consider the given equation above
Simplify the numerator in order to avoid the confusion later for differentiation, we have
Take the derivative of the above equation with respect to x
If x = 1, then the value of y' is equal to
"Published in Newark, California, USA"
Find y' for the given value of x for
Solution:
Consider the given equation above
Simplify the numerator in order to avoid the confusion later for differentiation, we have
Take the derivative of the above equation with respect to x
If x = 1, then the value of y' is equal to
Saturday, May 25, 2013
Implicit Differentiation
Category: Differential Calculus, Algebra
"Published in Suisun City, California, USA"
Find y" by implicit differentiation for
Solution:
Consider the given equation above
Since the given equation above is not a function, then we have to differentiate it by implicit differentiation as follows
but
or
then the above equation becomes
Rationalize the denominator in order to eliminate the radical sign at the denominator, we have
Take the derivative with respect to x, we have
Rationalize the denominator in order to eliminate the radical sign at the denominator, we have
Therefore,
"Published in Suisun City, California, USA"
Find y" by implicit differentiation for
Solution:
Consider the given equation above
Since the given equation above is not a function, then we have to differentiate it by implicit differentiation as follows
but
or
then the above equation becomes
Rationalize the denominator in order to eliminate the radical sign at the denominator, we have
Take the derivative with respect to x, we have
Rationalize the denominator in order to eliminate the radical sign at the denominator, we have
Therefore,
Subscribe to:
Comments (Atom)