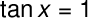Derivative - Exponential Functions, 2

Category: Differential Calculus, Algebra

"Published in Newark, California, USA"

Find the derivative for

Solution:

Consider the given equation above

The above equation is an exponential function but we cannot take the derivative by exponential function or even by power because the exponent of an algebraic function is also an algebraic function. In this type of exponential function, we need to take natural logarithm on both sides of an equation in order to eliminate the algebraic exponent of an algebraic function. 

Take natural logarithm on both sides on an equation, we have

Take the derivative on both sides of the equation with respect to x

Multiply on both sides of the equation by y

but 

Hence, the above equation becomes

Therefore, the final answer is

Integration - Exponential Functions

Category: Integral Calculus, Algebra

"Published in Newark, California, USA"

Evaluate

Solution:

Consider the given equation above

Since 3 and e have the same exponent which is x, then we can rewrite the above equation as follows

If

then

Apply the Integration of Exponential Functions to the above equation, we have

Apply the Laws of Logarithm for the product of coefficients at the denominator

Therefore, the final answer is

Solving Trigonometric Equations, 6

Category: Trigonometry

"Published in Suisun City, California, USA"

Solve for the value of x for

Solution:

Consider the given equation above

Rewrite secant, tangent, and cotangent into its equivalent function as follows

Divide both sides of the equation by sin x, we have

but

and the above equation becomes

Take the 4th root at both sides of the equation

Consider the positive value

Take the inverse tangent at both sides of the equation

Consider the negative value

Take the inverse tangent at both sides of the equation

Therefore, the final answers are

   

where n is the number of revolutions.