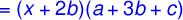Category: Algebra
"Published in Suisun City, California, USA"
Find the factors for
Solution:
Consider the given equation above
In factoring of any polynomial, we have to do the trial and error aside from inspecting the terms of a given equation. Well, let's do the grouping of the equation into two terms as follows
Remove the common factor of each group, we have
Since the three groups have their common factor which is (x + 2b), therefore, the factors of the given equation are

This website will show the principles of solving Math problems in Arithmetic, Algebra, Plane Geometry, Solid Geometry, Analytic Geometry, Trigonometry, Differential Calculus, Integral Calculus, Statistics, Differential Equations, Physics, Mechanics, Strength of Materials, and Chemical Engineering Math that we are using anywhere in everyday life. This website is also about the derivation of common formulas and equations. (Founded on September 28, 2012 in Newark, California, USA)
Saturday, November 2, 2013
Friday, November 1, 2013
Special Products - Factoring, 21
Category: Algebra
"Published in Newark, California, USA"
Find the factors for
Solution:
Consider the given equation above
You notice that there are five terms at the given equation, which means that we have to group three terms and then another group for the rest of the terms. If you look at the given equation, the first two terms and the last term will be a perfect trinomial square if you group them. Let's arrange the given equation and group the terms as follows
Take out their common factor which is (m - 2n), and therefore, the factors of the given equation are
"Published in Newark, California, USA"
Find the factors for
Solution:
Consider the given equation above
You notice that there are five terms at the given equation, which means that we have to group three terms and then another group for the rest of the terms. If you look at the given equation, the first two terms and the last term will be a perfect trinomial square if you group them. Let's arrange the given equation and group the terms as follows
Take out their common factor which is (m - 2n), and therefore, the factors of the given equation are
Thursday, October 31, 2013
Special Products - Factoring, 20
Category: Algebra
"Published in Newark, California, USA"
Find the factors for
Solution:
Consider the given equation above
In this type of factoring of a polynomial, grouping is needed and we need to group the terms according to their type of variables. In grouping, usually you have to do the trial and error until you get the desired factors. Let's group the first two terms and then another group for the remaining terms as follows
The first group can be factored by the difference of two squares while the other group can be factored by removing of their common factor. Let's factor the grouped terms as follows
The common factor of the above equation is (6x - 5y). Take out their common factor and therefore, the factors of the given equation are
"Published in Newark, California, USA"
Find the factors for
Solution:
Consider the given equation above
In this type of factoring of a polynomial, grouping is needed and we need to group the terms according to their type of variables. In grouping, usually you have to do the trial and error until you get the desired factors. Let's group the first two terms and then another group for the remaining terms as follows
The first group can be factored by the difference of two squares while the other group can be factored by removing of their common factor. Let's factor the grouped terms as follows
The common factor of the above equation is (6x - 5y). Take out their common factor and therefore, the factors of the given equation are
Subscribe to:
Comments (Atom)