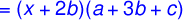Category: Algebra
"Published in Suisun City, California, USA"
Find the factors for
Solution:
Consider the given equation above
Did you notice that the first three terms of the given equation is a perfect trinomial square? Well, let's group the first three terms as follows
At the last three terms, when you group and take out their negative sign, then it will be a perfect trinomial square, too as follows
Next, rewrite the grouped terms in terms of exponential function as follows
Since the above equation can be factored by the difference of two squares in which the grouped terms are considered as a single term, then the factors of the given equation are

This website will show the principles of solving Math problems in Arithmetic, Algebra, Plane Geometry, Solid Geometry, Analytic Geometry, Trigonometry, Differential Calculus, Integral Calculus, Statistics, Differential Equations, Physics, Mechanics, Strength of Materials, and Chemical Engineering Math that we are using anywhere in everyday life. This website is also about the derivation of common formulas and equations. (Founded on September 28, 2012 in Newark, California, USA)
Monday, November 4, 2013
Sunday, November 3, 2013
Special Products - Factoring, 23
Category: Algebra
"Published in Suisun City, California, USA"
Find the factors for
Solution:
Consider the given equation above
Did you notice that the first four terms of the given equation is a perfect cube? Well, let's group the first four terms as follows
Next, rewrite the grouped terms in terms of exponential function as follows
Since 64 is a perfect cube, then we can factor the above equation by the difference of two cubes. Therefore, the factors of the given equation are
"Published in Suisun City, California, USA"
Find the factors for
Solution:
Consider the given equation above
Did you notice that the first four terms of the given equation is a perfect cube? Well, let's group the first four terms as follows
Next, rewrite the grouped terms in terms of exponential function as follows
Since 64 is a perfect cube, then we can factor the above equation by the difference of two cubes. Therefore, the factors of the given equation are
Saturday, November 2, 2013
Special Products - Factoring, 22
Category: Algebra
"Published in Suisun City, California, USA"
Find the factors for
Solution:
Consider the given equation above
In factoring of any polynomial, we have to do the trial and error aside from inspecting the terms of a given equation. Well, let's do the grouping of the equation into two terms as follows
Remove the common factor of each group, we have
Since the three groups have their common factor which is (x + 2b), therefore, the factors of the given equation are
"Published in Suisun City, California, USA"
Find the factors for
Solution:
Consider the given equation above
In factoring of any polynomial, we have to do the trial and error aside from inspecting the terms of a given equation. Well, let's do the grouping of the equation into two terms as follows
Remove the common factor of each group, we have
Since the three groups have their common factor which is (x + 2b), therefore, the factors of the given equation are
Subscribe to:
Comments (Atom)