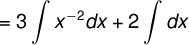Category: Integral Calculus
"Published in Newark, California, USA"
Evaluate
Solution:
Consider the given equation above
Since the term inside the square root sign is also x, then we can rewrite the given equation as follows
Apply the integration by power formula, we have
Therefore, the answer is
where C is the constant of integration.

This website will show the principles of solving Math problems in Arithmetic, Algebra, Plane Geometry, Solid Geometry, Analytic Geometry, Trigonometry, Differential Calculus, Integral Calculus, Statistics, Differential Equations, Physics, Mechanics, Strength of Materials, and Chemical Engineering Math that we are using anywhere in everyday life. This website is also about the derivation of common formulas and equations. (Founded on September 28, 2012 in Newark, California, USA)
Saturday, December 21, 2013
Friday, December 20, 2013
Integration - Algebraic Functions, Powers, 10
Category: Integral Calculus
"Published in Newark, California, USA"
Evaluate
Solution:
Consider the given equation above
The first thing that we have to do is to square the given equation as follows
Apply the integration by power formula, we have
Therefore, the answer is
where C is the constant of integration.
"Published in Newark, California, USA"
Evaluate
Solution:
Consider the given equation above
The first thing that we have to do is to square the given equation as follows
Apply the integration by power formula, we have
Therefore, the answer is
where C is the constant of integration.
Thursday, December 19, 2013
Integration - Algebraic Functions, Powers, 9
Category: Integral Calculus
"Published in Newark, California, USA"
Evaluate
Solution:
Consider the given equation above
Since the denominator consists of only one term, then we can rewrite the given equation as follows
Apply the integration by power formula, we have
Therefore, the answer is
where C is the constant of integration.
"Published in Newark, California, USA"
Evaluate
Solution:
Consider the given equation above
Since the denominator consists of only one term, then we can rewrite the given equation as follows
Apply the integration by power formula, we have
Therefore, the answer is
where C is the constant of integration.
Subscribe to:
Comments (Atom)