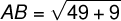"Published in Newark, California, USA"
Show that the points (5, 4), (-2, 1), and (2, -3) are the vertices of an isosceles triangle, and find its area.
Solution:
To illustrate the problem, it is better to draw the figure as follows
 |
| Photo by Math Principles in Everyday Life |
The first thing that we need to do is to get the length of the sides of a triangle using the distance of two points as follows
For the length of AB:
For the length of AC:
For the length of BC:
Since AB ≅ AC, then the given triangle is an isosceles triangle.
The area of a triangle is given by the formula
Substitute the values of the coordinates of the vertices of a triangle to the above equation and solve for the value of matrix or determinant, we have
Therefore, the area of a triangle is