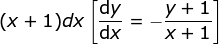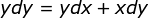Category: Differential Equations
"Published in Newark, California, USA"
Find the equation of a curve whose slope at any point is equal to - (y + 1)/(x + 1) and which passes through the point (0, 0).
Solution:
The
slope of a curve is equal to the first derivative of a curve with
respect to x. In this case, y' = dy/dx. Let's consider the given slope
of a curve
Multiply both sides of the equation by (x + 1)dx, we have
Integrate on both sides of the equation, we have
In
order to get the value of arbitrary constant, substitute the value of
the given point which is P(0, 0) to the above equation, we have
Therefore, the equation of a curve is

This website will show the principles of solving Math problems in Arithmetic, Algebra, Plane Geometry, Solid Geometry, Analytic Geometry, Trigonometry, Differential Calculus, Integral Calculus, Statistics, Differential Equations, Physics, Mechanics, Strength of Materials, and Chemical Engineering Math that we are using anywhere in everyday life. This website is also about the derivation of common formulas and equations. (Founded on September 28, 2012 in Newark, California, USA)
Tuesday, August 5, 2014
Monday, August 4, 2014
Finding the Equation of a Curve, 15
Category: Differential Equations
"Published in Newark, California, USA"
Find the equation of a curve whose slope at any point is equal to y/(y - x) and which passes thru the point (-1, 2).
Solution:
The slope of a curve is equal to the first derivative of a curve with respect to x. In this case, y' = dy/dx. Let's consider the given slope of a curve
Multiply both sides of the equation by (y - x)dx, we have
Integrate on both sides of the equation, we have
In order to get the value of arbitrary constant, substitute the value of the given point which is P(-1, 2) to the above equation, we have
Therefore, the equation of a curve is
"Published in Newark, California, USA"
Find the equation of a curve whose slope at any point is equal to y/(y - x) and which passes thru the point (-1, 2).
Solution:
The slope of a curve is equal to the first derivative of a curve with respect to x. In this case, y' = dy/dx. Let's consider the given slope of a curve
Multiply both sides of the equation by (y - x)dx, we have
Integrate on both sides of the equation, we have
In order to get the value of arbitrary constant, substitute the value of the given point which is P(-1, 2) to the above equation, we have
Therefore, the equation of a curve is
Sunday, August 3, 2014
Separation of Variables - Arbitrary Constant, 5
Category: Differential Equations
"Published in Newark, California, USA"
Find the particular solution for
in which y = 1 when x = 0.
Solution:
Consider the given equation above
In order to separate dx and dy from other variables, divide both sides of the equation by (x + 1)(y + 1) as follows
Integrate both sides of the equation, we have
Substitute the value of x and y in order to get the value of C as follows
Therefore, the particular solution is
"Published in Newark, California, USA"
Find the particular solution for
in which y = 1 when x = 0.
Solution:
Consider the given equation above
In order to separate dx and dy from other variables, divide both sides of the equation by (x + 1)(y + 1) as follows
Integrate both sides of the equation, we have
Substitute the value of x and y in order to get the value of C as follows
Therefore, the particular solution is
Subscribe to:
Comments (Atom)