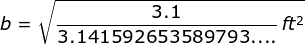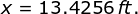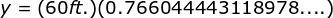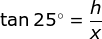More Cylinder Problems

Category: Solid Geometry

"Published in Newark, California, USA"

A vertical stone column 12.5 ft. high has an elliptical base with the longer axis twice the shorter. If the weight of the column is 12,400 lbs. and if the stone weighs 160 lbs. per cu. ft., find the area of the largest and smallest axial section of the column.

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The area of the ellipse which is the base of the column is

but

Hence, the above equation becomes

The volume of the column which is a cylinder is

The length of b which is the semi-minor axis of the ellipse is 

The length of a which is the semi-major axis of the ellipse is

Therefore, the area of the largest axial section of the column which is a rectangle is

Photo by Math Principles in Everyday Life

and the area of the smallest axial section of the column which is a rectangle is

Photo by Math Principles in Everyday Life

Trapezoid Prism Problems, 4

Category: Solid Geometry

"Published in Newark, California, USA"

A dam 100 ft. long has a cross section which is a trapezoid whose altitude is 16 ft., and whose upper base is 5 ft. If the lower base angles of the cross section are 50° and 65°, find the volume of material the dam contains.

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

Since the length of the lower base is not given, then we have to isolate the base first and then label further so that we can solve for its length.

Photo by Math Principles in Everyday Life

Consider the 50° right triangle,

 
Consider the 65° right triangle,

The length of the lower base of a trapezoid which is the cross section of a dam is

 

 

Hence, the area of the base is

Therefore, the volume of a trapezoid prism which is a dam is

Triangular Prism Problems, 5

Category: Solid Geometry

"Published in Newark, California, USA"

The Pennsylvania Railroad found it necessary, owing to land slides upon the roadbed, to reduce the angle of inclination of one bank of a certain railway cut near Pittsburgh, PA, from an original angle of 40° to a new angle of 25°. The bank as it originally stood was 200 ft. long and had a slant length of 60 ft. Find the amount of the earth removed, if the top level of the bank remained unchanged. 

Photo by Math Principles in Everyday Life

Solution:

Consider the given figure above

Photo by Math Principles in Everyday Life

From the two upper vertices of a triangle, draw vertical lines perpendicular to the ground and then label further the figure as follows

Photo by Math Principles in Everyday Life

Consider a 40° right triangle,

The value of h in a 25° right triangle is equal to the value of h in a 40° right triangle.

Consider a 25° right triangle,

The length of the base of an obtuse triangle is

The area of an obtuse triangle which is the base of the prism is

Therefore, the amount of earth removed which is the volume of a prism is