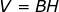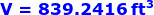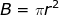Category: Chemical Engineering Math
"Published in Newark, California, USA"
Calculate the mole fractions of ethyl alcohol, C2H5OH, and water in a solution made by dissolving 9.2 grams of alcohol in 18 grams of H2O. (Atomic Weights: H = 1, C = 12, and O = 16)
Solution:
There are two substances or components in a solution which are ethyl alcohol (solute) and water (solvent). The first thing that we need to do is to get the molecular weight of each component.
Molecular Weight of Ethyl Alcohol:
Molecular Weight of Water:
Next, we can get the moles of each component since we know their molecular weights.
Moles of Ethyl Alcohol:
Moles of Water:
Therefore, the mole fraction of ethyl alcohol is
and the mole fraction of water is
Note: Mole fractions are unitless and the sum of the mole fractions of components in a solution must be equal to 1.

This website will show the principles of solving Math problems in Arithmetic, Algebra, Plane Geometry, Solid Geometry, Analytic Geometry, Trigonometry, Differential Calculus, Integral Calculus, Statistics, Differential Equations, Physics, Mechanics, Strength of Materials, and Chemical Engineering Math that we are using anywhere in everyday life. This website is also about the derivation of common formulas and equations. (Founded on September 28, 2012 in Newark, California, USA)
Wednesday, September 3, 2014
Tuesday, September 2, 2014
More Cylinder Problems, 13
Category: Solid Geometry
"Published in Vacaville, California, USA"
The outer protective smokestack of a steamship is streamlined so that it has a uniform oval section parallel to the deck. The area of this oval section is 48 sq. ft. If the length of the stack is 18 ft. and if the axis is raked 76°15' to the horizontal, find the volume enclosed by the stack. (Raked means inclined.)
Solution:
To illustrate the problem, it is better to draw the figure as follows
The area of a base which is an oval section is already given in the problem. By using a trigonometric function of a right triangle, the altitude of the smokestack is
Therefore, the volume of a smokestack which is a cylinder is
"Published in Vacaville, California, USA"
The outer protective smokestack of a steamship is streamlined so that it has a uniform oval section parallel to the deck. The area of this oval section is 48 sq. ft. If the length of the stack is 18 ft. and if the axis is raked 76°15' to the horizontal, find the volume enclosed by the stack. (Raked means inclined.)
Solution:
To illustrate the problem, it is better to draw the figure as follows
 |
| Photo by Math Principles in Everyday Life |
The area of a base which is an oval section is already given in the problem. By using a trigonometric function of a right triangle, the altitude of the smokestack is
Therefore, the volume of a smokestack which is a cylinder is
Monday, September 1, 2014
More Cylinder Problems, 12
Category: Solid Geometry
"Published in Vacaville, California, USA"
A cylinder whose base is a circle is circumscribed about a right prism of altitude 12.6 ft. Find the volume of the cylinder if the base of the prism is an isosceles triangle of sides 3 ft., 3 ft., and 2 ft.
Solution:
To illustrate the problem, it is better to draw the figure as follows
Consider the base of a cylinder which is a circle that circumscribed about an isosceles triangle as follows
The point of intersection of the perpendicular line bisectors of the sides of an isosceles triangle is also the center of a circle. The radius of a circle is equal to the distance from the point of intersection of the perpendicular line bisectors of the sides of an isosceles triangle to its vertex. By using trigonometric functions of right triangles, we can solve for the radius of a circle as follows
Hence, the radius of a circle is
Therefore, the volume of a circular cylinder is
But
Hence, the above equation becomes
"Published in Vacaville, California, USA"
A cylinder whose base is a circle is circumscribed about a right prism of altitude 12.6 ft. Find the volume of the cylinder if the base of the prism is an isosceles triangle of sides 3 ft., 3 ft., and 2 ft.
Solution:
To illustrate the problem, it is better to draw the figure as follows
 |
| Photo by Math Principles in Everyday Life |
Consider the base of a cylinder which is a circle that circumscribed about an isosceles triangle as follows
 |
| Photo by Math Principles in Everyday Life |
The point of intersection of the perpendicular line bisectors of the sides of an isosceles triangle is also the center of a circle. The radius of a circle is equal to the distance from the point of intersection of the perpendicular line bisectors of the sides of an isosceles triangle to its vertex. By using trigonometric functions of right triangles, we can solve for the radius of a circle as follows
Hence, the radius of a circle is
Therefore, the volume of a circular cylinder is
But
Hence, the above equation becomes
Subscribe to:
Posts (Atom)