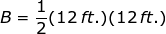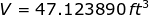Trapezoid Prism Problems, 5

Category: Solid Geometry

"Published in Vacaville, California, USA"

A trench is 200 ft. long and 12 ft. deep, 8 ft. wide at the top and 4 ft. wide at the bottom. How many cubic yards of earth have been recovered?

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The area of the base which is the area of the cross section of a trapezoid prism is

Therefore, the volume of earth removed from a trench which is the volume of trapezoid prism is

                          or

Right Circular Cylinder Problems, 15

Category: Solid Geometry

"Published in Newark, California, USA"

Find the volume of the largest right circular cylinder that can be circumscribed about a rectangular parallelepiped of dimensions 2 ft. by 3 ft. by 4 ft.

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

There are three ways in finding the volume of a right circular cylinder that circumscribed about a rectangular parallelepiped but we have to choose the largest volume.

If a = 2 ft., b = 3 ft., and c = 4 ft., then the volume of a right circular cylinder is

 

 

 

 

 

If a = 3 ft., b = 2 ft., and c = 4 ft., then the volume of a right circular cylinder is

If a = 2 ft., b = 4 ft., and c = 3 ft., then the volume of a right circular cylinder is

Therefore, the volume of the largest right circular cylinder that can be circumscribed about a rectangular parallelepiped is .

Right Circular Cylinder Problems, 14

Category: Solid Geometry

"Published in Newark, California, USA"

Pass a plane through a cube of edge 6 in. so that the section formed will be a regular hexagon. Find the volume of a right circular cylinder 8 in. long, (a) whose base circumscribed this hexagon, (b) whose base is inscribed in this hexagon.

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

If a cube is cut by a plane that passes through the midpoints of two adjacent sides from the upper base to the opposite lower base with the midpoints of two adjacent sides, then the intersection is a regular hexagon. By Pythagorean Theorem, the length of the sides of a regular hexagon is

 
Let's consider the section of a cube which is a regular hexagon as follows

Photo by Math Principles in Everyday Life

There are six equal equilateral triangles in a regular hexagon in which their common vertex is a center of a regular hexagon. All sides of equilateral triangles are all equal which are 3√2 in.

(a) If the base of a right circular cylinder circumscribes the regular hexagon, then the radius is equal to 3√2 in. A circle contains all the vertices of a regular hexagon. Therefore, the volume of a right circular cylinder is
 

 

 

 

(b) If the base of a right circular cylinder inscribes the regular hexagon, then the radius is tangent to all the sides of a regular hexagon. The radius of a right circular cylinder is also an apothem of a regular hexagon and an altitude of an equilateral triangle. The altitude of an equilateral triangle bisects its base. By Pythagorean Theorem, the radius of a right circular cylinder is

Therefore, the volume of a right circular cylinder is