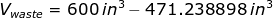Right Circular Cylinder Problems, 18

Category: Solid Geometry

"Published in Newark, California, USA"

How much wood is wasted in turning out the largest possible cylindrical rod from a stick whose uniform square cross-sectional area is 10 sq. in. and whose length is 5 ft.?

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

In this problem, the diameter of a circle is not given. Since the area of a cross-section of a stick is given which is a square, then we can solve for the sides of a square which is also a diameter of a circle as follows

Therefore, the amount of wood wasted in turning out the largest possible cylindrical rod from a stick is

Right Circular Cylinder Problems, 17

Category: Solid Geometry

"Published in Newark, California, USA"

A cylindrical tin can holding 2 gal. has its height equal to the diameter of its base. Another cylindrical tin can with the same capacity has its height equal to twice the diameter of its base. Find the ratio of the amount of tin required for making the two cans with covers.

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The volume of a tin can in cubic inches is

If the height of a tin can equals its diameter, then the diameter is

Hence, the total area of a tin can is

If the height of a tin can is twice its diameter, then the diameter is 

Hence, the total area of a tin can is 

Therefore, the ratio of the amount of tin required for making the two cans with covers is 

Rectangular Parallelepiped Problem, 15

Category: Solid Geometry

"Published in Newark, California, USA"

Two rectangular water tanks with tops on the same level are connected by a pipe through their bottoms. The base of one is 6 in. higher than that of the other. Their dimensions are 4 ft. by 5 ft. by 2½ ft. and 4 ft. by 7 ft. by 3 ft., respectively. How deep is the water in the larger tank when the water they contain equals half their combined capacity, if the 2½ ft. and 3 ft. edges are vertical?

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The total volume of two empty rectangular water tanks is

If two tanks are filled with water which is equal to one-half of the total volume of two empty tanks, the above figure becomes

Photo by Math Principles in Everyday Life

Therefore, from the figure above, the depth or height of water in the larger tank is