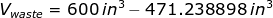"Published in Newark, California, USA"
How long a wire 0.1 in. in diameter can be drawn from a block of copper 2 in. by 4 in. by 6 in.?
Solution:
To illustrate the problem, it is better to draw the figure as follows
 |
| Photo by Math Principles in Everyday Life |
The volume of a block of copper is
Therefore, the length of a wire that can be drawn from a block of copper assuming that a wire is a right circular cylinder is equal to
or