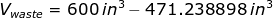Right Circular Cylinder Problems, 20

Category: Solid Geometry

"Published in Newark, California, USA"

A piece of lead pipe is 50 ft. long. Its outer radius is 2 in., and it is ¼ in. thick. Into how many spherical bullets ¼ in. in diameter can be melted?

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

If the thickness of a lead pipe is ¼ in., then the inner radius is

Hence, the volume of a lead pipe is

If a lead pipe is melted and then converted into spherical bullets of diameter ¼ in., the volume of a piece of spherical bullet is

 

 

 

Therefore, the number of spherical bullets in a lead pipe is
 

 

 

Right Circular Cylinder Problems, 19

Category: Solid Geometry

"Published in Newark, California, USA"

How long a wire 0.1 in. in diameter can be drawn from a block of copper 2 in. by 4 in. by 6 in.?

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The volume of a block of copper is

   

Therefore, the length of a wire that can be drawn from a block of copper assuming that a wire is a right circular cylinder is equal to

                       or

 

Right Circular Cylinder Problems, 18

Category: Solid Geometry

"Published in Newark, California, USA"

How much wood is wasted in turning out the largest possible cylindrical rod from a stick whose uniform square cross-sectional area is 10 sq. in. and whose length is 5 ft.?

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

In this problem, the diameter of a circle is not given. Since the area of a cross-section of a stick is given which is a square, then we can solve for the sides of a square which is also a diameter of a circle as follows

Therefore, the amount of wood wasted in turning out the largest possible cylindrical rod from a stick is