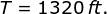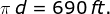Circle Inscribed - Triangle Problems

Category: Plane Geometry

"Published in Newark, California, USA"

The base of an isosceles triangle is 16 in. and the altitude is 15 in. Find the radius of the inscribed circle.

Solution:

To illustrate the problem, it is better to draw the figure as follows

Photo by Math Principles in Everyday Life

The area of ∆ABC is

Photo by Math Principles in Everyday Life

By using Pythagorean Theorem, we can solve for the two legs of an isosceles triangle as follows

Next, draw the angle bisectors of an isosceles traingle as follows

Photo by Math Principles in Everyday Life

The intersection of the angle bisectors of an isosceles triangle is the center of an inscribed circle which is point O. From point O, draw a line which is perpendicular to AB, draw a line which is perpendicular to AC, and draw a line which is perpendicular to BC. These three lines will be the radius of a circle. 

Photo by Math Principles in Everyday Life

The total area of an isosceles triangle is equal to the area of three triangles whose vertex is point O. Therefore, the radius of an inscribed circle is

Circle - Rectangle Problems

Category: Plane Geometry

"Published in Newark, California, USA"

The quarter mile race track shown in the figure has parallel sides AB and CD, each 315 ft. long. If the ends are semicircles, find the area bounded by the track. If a race is run from S to D by way of C, find the length of the race in yards, given that arc SC = 44/67 x arc AC. (1 mile = 5280 ft.)

Photo by Math Principles in Everyday Life

Solution:

The quarter mile race track consists of  two semicircles and a rectangle. Let's divide the given figure as follows

Photo by Math Principles in Everyday Life

Let T = be the total distance of a race which is equal to 0.25 miles
      d = be the diameter of the semicircles
      C = circumference of a circle which is equal to the total  length of two arcs of semicircles
      A = total area of a quarter mile race track
      
The total distance of a race in feet is equal to

The total distance of a race is

The total length of the two semicircles is equal to the circumference of a circle because the diameter of the two semicircles is the same which is d. The diameter of the two semicircles or the width of a rectangle is equal to

The total area of a quarter mile race is

The length of a race from S to D by way of C in feet is equal to

The length of a race from S to D by way of C in yards is equal to

 

Trapezoid, Quadrilateral Problems, 3

Category: Plane Geometry

"Published in Newark, California, USA"

Find the area of the rectilinear figure shown, if it is the difference between two isosceles trapezoids whose corresponding sides area parallel.

Photo by Math Principles in Everyday Life

Solution:

The given plane figure consists of the difference of two isosceles trapezoids. Let's analyze and label further the above figure as follows

Photo by Math Principles in Everyday Life

The area of a large trapezoid is

Before we solve for the area of a small trapezoid, we need to solve for the variables first.

Using Pythagorean Theorem

The height of a small trapezoid is

Since the given two trapezoids are isosceles trapezoid with the common thickness which is 2", then we can solve for the variables by using similar triangles. 

Using similar triangles

The length of the upper base of a small trapezoid is

Using similar triangles

The length of the lower base of a small trapezoid is

Hence, the area of a small trapezoid is

Therefore, the area of a plane figure is