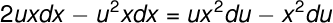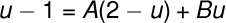Math Principles

Wednesday, July 24, 2013

Homogeneous Functions - Arbitrary Constant, 2

Category: Differential Equations, Analytic Geometry, Integral Calculus

"Published in Newark, Callifornia, USA"

Find the equation of a curve whose slope at any point is equal to y/(y - x) and which passes through the point (-1, 2).

Solution:

If you want get the slope of a curve at any point whose variables are second degree, third degree, fourth degree, and so on, then you need to take the first derivative of a curve with respect to an independent variable which is x in common. In this case, the given slope of a curve can be written as

The above equation cannot be solved by Separation of Variables because dy is multiplied by (y - x) and there's no way to separate the variables. This type of equation is Homogeneous Function. We have to substitute a variable with another variable first in order to solve the given equation by Separation of Variables as follows:

Let

so that

Substitute the value of y and dy to the above equation, we have

The above equation can now be solved by Separation of Variables as follows

Since the right side of the equation is a rational function in which the denominator has two factors, then it must be expressed into partial fractions:

Multiply both sides of the equation by their Least Common Denominator (LCD) which is u(2 - u), we have

Equate their u:

Equate their constants:

Substitute the value of A to other equation in order to solve for the value of B

Substitute the values of A and B to the original equation, we have

Integrate on both sides of the equation

Apply the laws of logarithm to the above equation

Take the inverse natural logarithm on both sides of the equation

Square on both sides of the equation

where C² = D

We know that

Substitute the value of u to the above equation, we have

But x = -1 and y = 2 from the given point of a curve which is (-1, 2), then the value of D will be equal to

Therefore, the equation of a curve that passes thru the point (-1, 2) is

Tuesday, July 23, 2013

Two Intersecting Lines, 3

Category: Analytic Geometry, Algebra

"Published in Newark, California, USA"

Find the equation of a line that passes through the intersection of x - y = 0 and 3x - 2y = 2 and forms a triangle at 1st Quadrant whose area is 9.

Solution:

To illustrate the problem, it is better to sketch the graph of two lines as follows:

For x - y = 0,

x - y = 0
y = x

slope (∆y/∆x), m = 1
y-intercept = 0

To trace the graph, plot 0 at the y-axis. This is your first point of the line (0, 0). Next, use the slope to get the second point. From the first point, count 1 unit to the right and then 1 unit upward.

For 3x - 2y = 2,

3x - 2y = 2
2y = 3x - 2
y = 3/2 x - 1

slope (∆y/∆x), m = 3/2
y-intercept = -1

To trace the graph, plot -1 at the y-axis. This is your first point of the line (0, -1). Next, use the slope to get the second point. From the first point, count 2 units to the right and then 3 units upward.

Photo by Math Principles in Everyday Life

To get their point of intersection, we have to use the two given equations and solve for x and y as follows

from

Substitute the second equation to the first equation, we have

Substitute x to either of the two equations,

Therefore, their point of intersection is P(2, 2).

Photo by Math Principles in Everyday Life

From the given word problem says "...forms a triangle at 1st Quadrant whose area is 9.", then the line that passes through point P will intersect at x-axis and y-axis. The resulting figure is a right triangle whose sides are x and y. The right angle is the origin while point P is located at the hypotenuse as follows