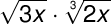Category: Algebra
"Published in Newark, California, USA"
Perform the indicated operations
Solution:
Consider the given equation above
If
you will multiply a radical with another radical with the same index,
then the terms inside the radicals will be multiplied together.
How about if you will multiply a radical with another radical with different index? If their indexes are different, then you cannot multiply the terms inside the radicals together. The given equation above is an example of multiplication of radicals with different indexes. The given equation above can be written as
Next, convert the exponential fractions into their common denominator by getting their Least Common Denominator (LCD) as follows
The LCD of 2 and 3 is 6. ½ becomes 3/6 (6 ÷ 2 x 1 = 3) and ⅓ becomes 2/6 (6 ÷ 3 x 1 = 2). The above equation can be written as
Since the index of the two radicals are now the same, then the terms inside the radicals can be multiplied together as follows
Therefore, the final answer is