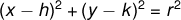"Published in Newark, California, USA"
Find the equation of a circle that is tangent to the line 4x - 3y + 10 = 0 and its center at (5, 5).
Solution:
To illustrate the problem, it is better to draw the figure as follows
 |
| Photo by Math Principles in Everyday Life |
The radius of a circle can be solved by using the perpendicular distance of a point to the line formula as follows
where A, B, and C are the coefficients of the equation of a given line. Hence, the above equation becomes
Since the coefficient of 10 is positive, then it follows that the sign of a radical is negative. Take the opposite sign of 10.
Substitute the values of x and y from the coordinates of a center of a circle, we have
The radius of a circle is always a positive value. We need to take the absolute value for that one. Hence, r = 3.
Therefore, the equation of a circle is