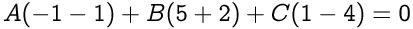Money - Investment Problem, 2

Category: Algebra

"Published in Newark, California, USA"

Aling Etang bought several dozen eggs at PHP 600. Because of poor storage, 2 dozens were spoiled and had to be thrown away. Nonetheless, she realized a profit of PHP 154 by charging PHP 3 more than she paid per dozen. How many dozen eggs did she buy?

Solution: 

The given word problem is about money and investment problem with profit, of course where she thrown 2 dozens of eggs but she earned a profit by charging more than she paid per dozen in order to save her capital or investment from loss. Let's analyze the problem as follows

Let x = be the price of a dozen of eggs, in PHP
      y = be the number of dozens of eggs

From the first word statement, "Aling Etang bought several dozen eggs at PHP 600", the working equation will be

From the next word statement, "Because of poor storage, 2 dozens were spoiled and had to be thrown away", the working equation will be

From the next word statement, "....by charging PHP 3 more than she paid per dozen," the working equation will be

The overall working equation for this problem is

               Profit = Total Amount Sold - Total Amount Invested

but

and

The above equation becomes

Divide both sides of the equation by -2, we have

Multiply both sides of the equation by x, we have

Use Quadratic Formula to solve for the value of x, we have

To calculate the price of a dozen of eggs, choose the positive sign as follows

Therefore, the price of a dozen of eggs is PHP 10. 

Consider the first equation

if x = 10, then 

Therefore, Aling Etang bought 60 dozens of eggs. 

Note: PHP means Philippine Pesos and the prices mentioned in the word problem above was in 1985. 

                      

Angle - Two Intersecting Curves

Category: Differential Calculus, Analytic Geometry, Algebra

"Published in Newark, California"

Find the angle of intersection between the pair of curves:

Solution:

To illustrate the problem, it is better to sketch the graph of two curves as follows

Photo by Math Principles in Everyday Life

Next, we need to get their point of intersection by solving the two systems of equations as follows

but

The above equation becomes

Using the second equation, the value of y is 2. Therefore, their point of intersection is (2, 2). Label further the figure as follows

Photo by Math Principles in Everyday Life

The slopes of two curves can be obtained by getting their derivative with respect to x as follows

for 

then

for

then

but x = 2 from their point of intersection, therefore

The angle of intersection is given by the formula

Substitute the values of m1 and m2 to the above equation, we have

Therefore,

or

Finding Equation - Plane

Category: Analytic Geometry, Algebra

"Published in Newark, California, USA"

Find the equation of a plane that contains the points (1, -2, 4), (4, 1, 7), and (-1, 5, 1).

Solution:

The first thing that we have to do is to write the equation of a plane that contains the first point as follows

Next, substitute the values of x, y, and z from the other two points to the above equation, we have

for (4, 1, 7), then the above equation becomes

or

for (-1, 5, 1), then the above equation becomes

If you add the two equations above, then we can solve for the value of A in terms of B as follows

Substitute the value of A to either of the two equations to solve for the value of C in terms of B as follows

Therefore, the equation of a plane is

    

Divide both sides of the equation by B and then simplify, we have

Photo by Math Principles in Everyday Life