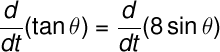Differentiation - Rate Problem, 2

Category: Differential Calculus, Trigonometry

"Published in Newark, California, USA"

If an angle θ increases uniformly, find the smallest positive value of θ for which tan θ increases 8 times as fast as sin θ. 

Solution:

The given word problem is about the rate problem of an angle θ and its trigonometric functions. 

From the word statement, "...for which tan θ increases 8 times as fast as sin θ." then the working equation will be

Take the derivative on both sides of the equation with respect to time t as follows

As you notice that we can cancel the angular rate which is ^dθ/_dt on both sides of the equation and we can solve for the value of angle θ as follows

Take the cube root on both sides on the equation, we have

Take the inverse cosine on both sides of the equation,

Therefore,

Proving Trigonometric Identities, 5

Category: Trigonometry

"Published in Newark, California, USA"

Prove that 

Solution:

Consider the give equation above

Use the left side of the equation to prove the trigonometric identities because it is more complicated part, as follows

Use the sum and product formula, we have

Multiply the numerator and the denominator by sin x, we have

but

Therefore the above equation becomes

Therefore,

Theory - Polynomial Equations

Category: Algebra

"Published in Newark, California, USA"

Form the equation of a polynomial if the roots are -3, 5, 6, -1, and -1. 

Solution:

The degree of a polynomial depends with the number of roots whether the roots are real numbers, irrational numbers, rational numbers, and complex numbers. In this case, if there are 5 roots in the given equation, then the degree of a polynomial must be 5 also. 

The number of terms of a polynomial is equal to the number of roots plus one. In this case, if there are 5 roots in the given equation, then the number of terms of a polynomial must be 6. 

If the roots are -3, 5, 6, -1, and -1, then the equation of a polynomial will be