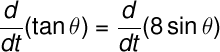"Published in Newark, California, USA"
If an angle θ increases uniformly, find the smallest positive value of θ for which tan θ increases 8 times as fast as sin θ.
Solution:
The given word problem is about the rate problem of an angle θ and its trigonometric functions.
From the word statement, "...for which tan θ increases 8 times as fast as sin θ." then the working equation will be
Take the derivative on both sides of the equation with respect to time t as follows
As you notice that we can cancel the angular rate which is dθ/dt on both sides of the equation and we can solve for the value of angle θ as follows
Take the cube root on both sides on the equation, we have
Take the inverse cosine on both sides of the equation,
Therefore,
