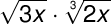Algebraic Operations - Radicals, 26

Category: Algebra

"Published in Newark, California, USA"

Perform the indicated operations

Solution:

Consider the given equation above

If you will multiply a radical with another radical with the same index, then the terms inside the radicals will be multiplied together.

How about if you will multiply a radical with another radical with different index? If their indexes are different, then you cannot multiply the terms inside the radicals together. The given equation above is an example of multiplication of radicals with different indexes. The given equation above can be written as

Next, convert the exponential fractions into their common denominator by getting their Least Common Denominator (LCD) as follows

The LCD of 2 and 3 is 6. ½ becomes 3/6 (6 ÷ 2 x 1 = 3) and ⅓ becomes 2/6 (6 ÷ 3 x 1 = 2). The above equation can be written as

Since the index of the two radicals are now the same, then the terms inside the radicals can be multiplied together as follows

Therefore, the final answer is

Algebraic Operations - Radicals, 25

Category: Algebra

"Published in Newark, California, USA"

Perform the indicated operations

Solution:

Consider the given equation above

The above equation can be written as

If you will multiply a radical with another radical with the same index, then the terms inside the radicals will be multiplied together.

As a rule in Mathematics, all radicals in the denominator should be rationalized or eliminated. This type of equation is a difficult one because both the numerator and the  denominator consist of a cube root of an equation and another number without a radical sign. We can eliminate the cube root sign at the denominator by applying the principles of Algebra which is the Sum and Difference of Two Cubes as follows

Apply the Distributive Property of Multiplication Over Addition at the numerator, we have

Therefore, the final answer is

Algebraic Operations - Radicals, 24

Category: Algebra, Arithmetic

"Published in Newark, California, USA"

Perform the indicated operations

Solution:

Consider the given equation above

The above equation can be written as

As a rule in Mathematics, all radicals in the denominator should be rationalized or eliminated. This type of equation is a difficult one because the denominator consists of two cube roots of numbers and another number without a radical sign. We can eliminate the cube root sign at the denominator by applying the principles of Algebra which is the Sum and Difference of Two Cubes although the above equation are all numerals in order to rationalize the denominator as follows

Therefore, the final answer is