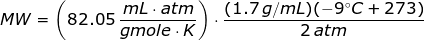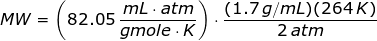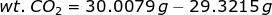Category: Chemical Engineering Math
"Published in Newark, California, USA"
The following data were obtained in the determination of a HC gas containing 92.3% C by weight at -9°C at various pressure:
| P (atm) |
1 |
2 |
3 |
| ρ (g/mL) |
1.45 |
1.7 |
1.95 |
Identify the gas.
Solution:
The given problem is about finding the molecular formula of a hydrocarbon gas using the principles of empirical and molecular formula. Since the given items are temperature, pressure, and density, then we have to use the Ideal Gas Law in order to get the molecular weight at different pressures and densities.
Let's consider the Ideal Gas Law equation:
but  and the above equation becomes
but
and the above equation becomes
but 
Hence, the Ideal Gas Law equation if the density is given is
where:
MW = molecular weight of unknown gas
ρ = is the density of unknown gas
R = universal gas law constant
T = absolute temperature of unknown gas
P = pressure of unknown gas
Since the units like K, mL, grams, gmoles, and atm are given,then the value of universal gas law constant is
Looking at the given table above, if you get the average of the given pressures and densities, then the value of P is 2 atm and the value of ρ is
1.7 g/mL.
The molecular weight of the unknown gas is
In one mole of unknown gas, the weight of C is
and the weight of H is
The number of moles of C is
and the number of moles of H is
In order to get the number of atoms of C and H, we need to divide them with the smallest number of moles. In this case, H has a number of smallest moles.
The number of C atoms is
and the number of H atoms is
Hence, the empirical formula of the unknown gas is CH.
Since CH is not a stable molecule, then we have to multiply both the number of C and H atoms by 2 in order to become a stable molecule. If you will follow the Octet Rule and Covalent Bonding, the number of electrons surrounding at each C atoms will be equal to eight.
Therefore, the molecular formula of the unknown gas is C2H2 which is acetylene.
Category: Chemical Engineering Math
"Published in Newark, California, USA"
When evacuated or empty, a gas density bulb weighs 29.3215 grams. First, CO2 gas was used to fill the bulb at 40°C and 1.0 atm pressure and it weighed 30.0079 grams. The bulb was then evacuated and filled with the mixture of CO and CO2 under the same temperature and pressure. With this mixture the bulb weighed 29.9332 grams. Determine the % of CO in the mixture.
Solution:
Since the temperature, pressure, and volume are all the same in both cases, then we don't have to use the Ideal Gas Law. We need to use only the principles of Mole Fractions.
Let's consider the first case. If a bulb is filled with CO2, then the weight of CO2 is
and the moles of CO2 is
Since the temperature, pressure, and volume are all the same in both cases, then it follows that
Next, for the second case, if a bulb is filled with a mixture of CO and CO2, then its weight is
Let x be the weight of CO in the mixture so that
Therefore, the weight percent of CO in the mixture is
Category: Chemical Engineering Math
"Published in Newark, California, USA"
A solution containing 4.48 ppm KMnO4 has a transmittance of 0.576 in a 1.00 cm cell at 520 nm. If the transmittance of an unknown solution is 0.735, what is the concentration of the unknown KMnO4 solution in ppm.
Solution:
The given word problem is about transmittance and absorbance problem in which we can get the concentration of any unknown solutions. Mostly, spectrophotometer is used in getting the concentration of unknown solutions including the blank sample and known sample. By Beer's Law, we can calculate the concentration of any unknown solutions as follows
where:
T = transmittance
A = absorbance
a = molar absorptivity
b = thickness of the cell
c = concentration of solution
If the transmittance of 4.48 ppm KMnO4 is 0.576, then the value of a which is the molar absorptivity is
If the value of transmittance for the unknown KMnO4 solution is 0.735, therefore, its concentration is