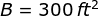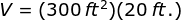"Published in Newark, California, USA"
(a) Find the volume of water in a swimming pool with vertical ends and sides. The length measured at the water line is 50 ft. and the breadth is 20 ft. The bottom of the swimming pool is a plane slopping gradually downward so that the depth of the water at one end is 4 ft. and at the other end is 8 ft.
(b) If the sides, ends, and bottom of the swimming pool are constructed of tile blocks whose glazed surface dimensions are 3 in. by 6 in., and if the ends and sides of the pool extend 2 ft. above the water level, find the number of blocks used if 1/20 of the surface area is covered by sealing material.
Solution:
(a) To illustrate the problem, it is better to draw the figure as follow
 |
| Photo by Math Principles in Everyday Life |
Did you notice that the swimming pool is a trapezoid prism whose two opposite faces are right trapezoid? Well, the area of the base which is a right trapezoid is
Therefore, the volume of water in a swimming pool which is a trapezoid prism is
(b) If the ends and sides of the pool extend 2 ft. above the water level, the dimensions of the pool are as follows
 |
| Photo by Math Principles in Everyday Life |
We need to get the unknown dimensions of the sides of the pool first so that we can solve for the total surface area of the pool especially the area of the bottom of the pool. Let's analyze a surface of the pool as follows
 |
| Photo by Math Principles in Everyday Life |
By Pythagorean Theorem,
Hence, the total surface area of the pool is
The total area of the sealing material used is
The total area of the tile blocks used is
The area of a tile block is
Therefore, the number of tile blocks used for the pool is
The number of tile blocks must be in whole numbers. We have to round off to the nearest ones. The answer is