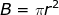"Published in Vacaville, California, USA"
A cylinder whose base is a circle is circumscribed about a right prism of altitude 12.6 ft. Find the volume of the cylinder if the base of the prism is an isosceles triangle of sides 3 ft., 3 ft., and 2 ft.
Solution:
To illustrate the problem, it is better to draw the figure as follows
 |
| Photo by Math Principles in Everyday Life |
Consider the base of a cylinder which is a circle that circumscribed about an isosceles triangle as follows
 |
| Photo by Math Principles in Everyday Life |
The point of intersection of the perpendicular line bisectors of the sides of an isosceles triangle is also the center of a circle. The radius of a circle is equal to the distance from the point of intersection of the perpendicular line bisectors of the sides of an isosceles triangle to its vertex. By using trigonometric functions of right triangles, we can solve for the radius of a circle as follows
Hence, the radius of a circle is
Therefore, the volume of a circular cylinder is
But
Hence, the above equation becomes