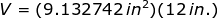"Published in Newark, California, USA"
The base of a right cylinder is shown in the figure. It is formed by describing semicircular arcs within the square upon the four sides as diameters. If the altitude of the cylinder is 12 in., find the volume and total area.
 |
| Photo by Math Principles in Everyday LIfe |
Solution:
Consider the given figure above
 |
| Photo by Math Principles in Everyday Life |
If you think that the given figure is difficult to get its length and area, then you are right. In this kind of figure, you need to use the principles of integral calculus in order to solve for the length of a curve as well as its area. Well, in this problem, we don't have to use the principles of integral calculus. The given figure consists of a square and the arcs of semicircles whose diameters are the sides of a square. Let's consider the semicircles at the left and right side as follows
 |
| Photo by Math Principles in Everyday Life |
The area of the unshaded region which is A is
Hence, the area of the base which is the four shaded area is
Therefore, the volume of a right cylinder whose base is the four shaded area is
If you look again the given figure, there are four semicircles enclosed the shaded region. The length or circumference of four semicircles is equivalent to the circumference of two circles. Hence, the circumference of two circles is
Therefore, the total area of a right cylinder whose base is the four shaded area is