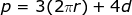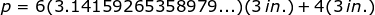"Published in Newark, California, USA"
Using the vertices of a 9-in. square as centers, and radii equal to 3 in., four arcs are described outside the square. If the figure thus formed is the uniform cross section of cylinder of element 7 in., find the volume and total area of the cylinder.
Solution:
To illustrate the problem, it is better to draw the figure which is the cross section as follows
 |
| Photo by Math Principles in Everyday Life |
As you can see from the figure above that there are four three-fourth circles. Hence, the area of the shaded region which is also the base of a right cylinder is
Therefore, the volume of a right cylinder is
Next, we need to get the perimeter of the base of the shaded region which is equal to the sum of the circumference of four three-fourth circles and the length of the four line segments between the arcs of three-fourth circles as follows
Hence, the surface or lateral area of a right cylinder is
Therefore, the total area of a circular cylinder is